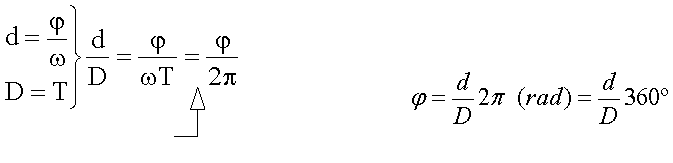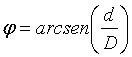PRÁCTICA
4
EL OSCILOSCOPIO. MEDIDA DE CORRIENTES VARIABLES.
INTRODUCCIÓN
Hasta este momento, hemos estado
trabajando con corriente continua, esto es, una corriente
eléctrica que se caracteriza por una
intensidad constante en el tiempo, y por lo tanto, por una diferencia
de potencial, entre dos puntos cualesquiera, que también lo
es. Sin embargo, en numerosas ocasiones nos encontraremos con
señales
sinusoidales ( corriente alterna ) y señales cuadradas,
entre otras.
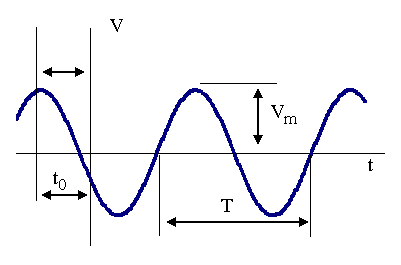
En las señales sinusoidales la intensidad sigue una
expresión dependiente del tiempo y de la forma i(t)=Imaxcos(ω
t+ φ i ) , y por lo tanto la tensión
tendrá una expresión similar: V(t)=Vmax
cos(ωt+ φu ) . Aparecen tres parámetros: la
intensidad o la tensión máxima o amplitud de la
señal ( Im o V m), la pulsación
(ω) y la fase inicial ( φi o φ u
).
En la figura se muestra la curva correspondiente a la función
sinusoidal, así como los parámetros de la misma.
Así, si somos capaces de representar la señal tal como
aparece en
la figura, la medida de la tensión máxima es inmediata,
mientras que la pulsación la podemos conocer a partir de la
medida
del periodo, T: conocido el periodo (en segundos), su
inversa en la frecuencia en herzios (f= 1/T) y la
pulsación se calcula a partir de la expresión ω=2πf
, siendo su unidad el radián. Si bien La medida de la fase
inicial se realizaría fácilmente sin más que
operar φ=ωt0 y teniendo en cuenta que es positiva
cuando el máximo se encuentra a la izquierda del eje de
ordenadas, si tenemos una única curva, dado que el origen de
tiempos es arbitrario, lo más cómodo es hacerlo coincidir
con el máximo de la señal y, por lo
tanto, fijar en φ =0 la fase inicial.
Podemos representar una diferencia de potencial
alterna, haciendo uso del osciloscopio. El osciloscopio es un
voltímetro que mide la variación con el tiempo de la
diferencia de potencial entre dos puntos. Tiene la posibilidad de medir
dos señales de forma simultánea.
En el enlace
“osciloscopio
” se explican las nociones básicas sobre el funcionamiento
interno
del osciloscopio, y se dan instrucciones sobre la utilización
del
osciloscopio
analógico Hameg. En esta
práctica vamos a hacer uso del osciloscopio
virtual. En este enlace
podéis encontrar un manual para aprender su
funcionamiento. En resumen, para su correcto uso e
instalación hay que tener en cuenta lo siguiente:
- Al
iniciar la medida, todos lo pulsadores han de estar hacia fuera y los
botones centrales de los mandos de amplitud y de base de tiempos en su
punto de calibración.
- La
conexión del circuito con el osciloscopio se realiza ha
través de un cable llamado BNC-bananas.
Las dos bananas se conectan a los puntos cuya diferencia de potencial
se desea medir. Hay que tener en cuenta que la banana negra, se
corresponde con la malla del cable que se une eléctricamente a
la masa carcasa del aparato y, por lo tanto, a tierra a través
de la conexión externa de la BNC: por lo tanto, la banana negra
está conectada a la tierra del laboratorio y este dato hay que
tenerlo en cuenta dado que un circuito eléctrico sólo
debería tener un nudo conectado a tierra. En caso contrario se
produce un cortocircuito entre los nudos conectados a tierra.
Para obtener
una señal sinusoidal haremos uso del generador de
señales, cuyo funcionamiento está explicado en el enlace generador de funciones.
En esta
práctica vamos a realizar circuitos de corriente alterna
mediante
el programa laboratorio virtual.
Puedes encontrar información sobre el funcionamiento del
programa en el enlace "ayuda laboratorio virtual".
CUESTIÓN 1. Realiza el circuito de la figura, consistente en un
generador de señales, un condensador de 4,4 ?F y una resistencia
de 120 ?, puestas en serie. Medirás la señal que
introduce el generador (la tensión sinusoidal) con un
osciloscopio analógico. Para ello conectaremos el canal 1 del
osciloscopio entre los terminales del generador:
(observa que el generador también se une al circuito con un
cable BNC-bananas y que la banana negra está unida a la tierra
del laboratorio a través del generador: luego ambas bananas
negras deben estar unidas al mismo punto del circuito. Este punto se ha
expresado con el símbolo de tierra en la figura. A la derecha
tienes una imagen más real del circuito que has de montar.
CUESTIÓN 1. Realiza el
circuito de la figura, consistente en un
generador de señales, un condensador de
4,4 μF y una resistencia de 120 Ω, puestas en serie. Medirás la
señal que
introduce el generador (la tensión sinusoidal) con un
osciloscopio
analógico. Para ello conectaremos el canal 1 del osciloscopio
entre los
terminales del generador:
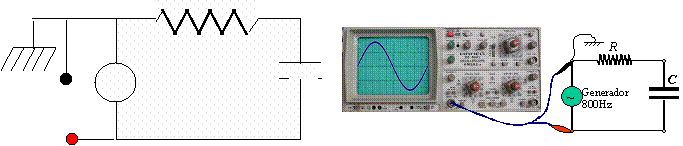
(Observa que el generador también se une al circuito con un
cable
BNC-bananas y que la banana negra está unida a la tierra del
laboratorio a través del generador: luego ambas bananas negras
deben
estar unidas al mismo punto del circuito. Este punto se ha expresado
con el símbolo de tierra en la figura). A la derecha tienes una
imagen
más real del circuito que has de montar.
Selecciona en el
generador la opción sinusoidal y fija en el generador de
señales una frecuencia de 800 Hz y una amplitud de 2 V. Para
ajusta la amplitud del generador, mídela con el osciloscopio
antes de montar el circuito. Una vez montado el circuito mide en el
osciloscopio ambos valores y compáralos con los solicitados:
Mide en el
osciloscopio la tensión y el periodo. A
partir del periodo, calcula la frecuencia y pulsación de la
señal. Completa la tabla siguiente.
|
Aplitud (V)
|
Periodo (ms)
|
Frecuencia (Hz)
|
Pulsación (rad)
|
Valor medido
|
|
|
|
|
¿Existe alguna diferencia entre el valor solicitado al generador
y el medido? Si es así, ¿cuál de los dos valores
darías por bueno? ¿Por qué?
CUESTIÓN 2. Dado que estamos midiendo una única
señal, el origen de tiempos lo podemos coger de tal forma que el
valor de la fase inicial, φ, sea nulo. De esta
forma ya conocemos los tres parámetros, amplitud,
pulsación y fase inicial, que nos permiten escribir la
función sinusoidal: V(t)=V max
cos(ωt+ φu).
Escribe
la función V(t) teniendo en cuenta los
parámetros calculados.
Vmax
|
ω
|
φu
|
V(t)=Vmax cos(ωt+ φu)
|
|
|
|
|
Una vez tienes la ecuación que representa la tensión
senoidal, la puedes reproducir fácilmente en una hoja de
cálculo.
CUESTIÓN 3. Un
multímetro, midiendo señales sinusoidales, mide el valor
eficaz de la señal, esto es, el valor máximo o amplitud
dividido por raíz de dos. Sin desmontar el circuito anterior,
mide con un multímetro la misma señal medida con el
osciloscopio, la tensión entre los bornes del generador. Para
ello debes conectar de forma adecuada el multímetro y elegir la
opción de medir tensión alterna.
Para verificar que la tensión medida en el multímetro es
la tensión eficaz de la señal medida, completa la tabla
siguiente
Amplitud medida(*) (Vmax)
|
Valor eficaz medido
(Ve)
|
Valor eficaz calculado
|
|
|
|
(*) rellenar con datos de
la tabla anterior
Conoceremos el comportamiento de un circuito eléctrico cuando
conozcamos dos magnitudes en el relacionadas: la tensión
y la intensidad. Por ello es usual que en el análisis de un
circuito se estudien se forma simultánea ambas magnitudes. De
hecho, para conocer el valor de una resistencia nos tocó medir
de forma simultánea tensión e intensidad. En el caso en
que tengamos corriente alterna, la necesidad de realizar medidas
simultáneas de ambas magnitudes viene agudizada por el hecho de
que ambas señales tiene fases iniciales diferentes, existiendo
por lo tanto un desfase entre ambas señales, (φu
-φi), que es necesario medir.
El osciloscopio, trabajando en forma dual, nos permite visualizar ambas
señales de forma simultánea y en tiempo real. De esta
forma podemos, además de medir cada una de las señales
conocer el desfase entre ambas. Dado que el osciloscopio mide
diferencias de potencial, para conocer la intensidad que circula
bastará con medir la diferencia de potencial entre los extremos
de una resistencia conocida, para a continuación aplicar la ley
de Ohm. Si en la medida anterior hemos medido la tensión de
entrada al circuito con el canal 1, si conectamos el canal 2 en bornes
de la resistencia podremos conocer la intensidad que circula por el
mismo.
Sin
desmontar el circuito anterior, conectaremos el canal dos del
osciloscopio entre los terminales de la resistencia:
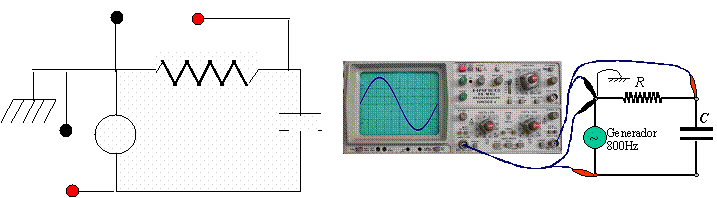
Tened en
cuenta que la banana negra del cable conectado al canal 2 está
conectada a su vez a la masa del aparato y a la tierra del circuito,
por lo que se debe conectar al mismo punto en el que se han conectado
el resto de bananas negras, esto es, a la tierra del circuito.
CUESTIÓN 4
: Una vez montado el circuito, selecciona el canal 2 y mide los valores
de la amplitud y la pulsación de la tensión en bornes de
la resistencia. Compáralos con los valores hallados
anteriormente para la tensión de entrada al circuito (canal 1):
|
Aplitud (V)
|
Periodo (ms)
|
Frecuencia (Hz)
|
Pulsación (rad)
|
d.d.p. entrada (Canal 1)(*)
|
|
|
|
|
d.d.p. resistencia (Canal 2)
|
|
|
|
|
(*) rellenar
con datos de la medida anterior
Hasta aquí
has estudiado cada tensión por separado. Pero si las representas
juntas (modo dual) verás que una aparece retrasada respecto de
la otra: existe un desfase entre ambas, dado que las fases iniciales
de ambas señales son diferentes.
Para poder conocer el comportamiento del circuito es muy importante
medir este desfase. Tendremos dos formas para hacerlo. La
utilización de un método u otro vendrá dada por la
mayor precisión en la medida o por la mayor rapidez. Una primera
forma de medida del desfase será a partir de la
representación de ambas señales juntas. Para ello debes
poner el osciloscopio en forma dual: aparecerán en pantalla
ambas señales en un mismo eje de tiempos. Supongamos que las
curvas medidas en el cana1 y en el canal 2 son las de la figura:
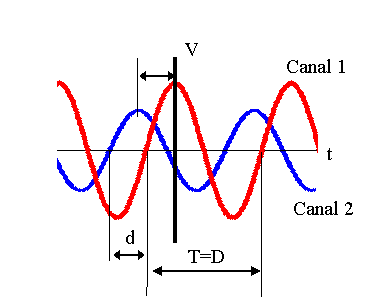
La
separación entre los máximos de ambas señales se
corresponde con el valor φ/ω. Este valor es igual a la distancia, en
segundos, que separa los puntos homólogos de ambas curvas en su
corte con el eje de abscisas: d.
Por otra parte el periodo de la señal se corresponde con la
distancia
D, medida en segundos. Luego:
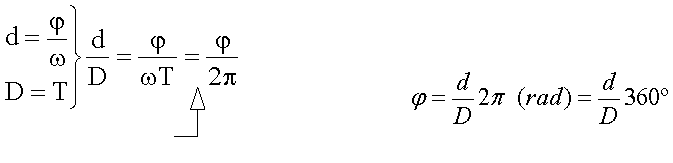
Podemos calcular fácilmente el valor del desfase
sin más que medir las distancias d y D, que pueden medirse tanto
en segundos como en centímetros, dado que la relación
entre ambas es un número adimensional. Falta conocer el signo de
dicho desfase. En
la figura, el máximo del canal 1 coincide con el origen de
tiempos,
luego φ1 = 0, y la fase del canal 2 aparece a la izquierda
del
origen de tiempo, luego φ2 > 0: El desfase en mayor que
cero,
φ=φ 2-φ1>0. Diremos que la señal del
canal
2 está adelantada respecto la señal del canal 1, dado que
su
máximo aparece a tiempo menores.
CUESTIÓN 5. Mide el desfase de ambas
señales por el método “dual”. Dibuja en el gráfico
las señales visualizadas en pantalla y desarrolla claramente
todo el proceso de cálculo. Recuerda que en el dibujo las
escalas de ambas señales deben ser las mismas y obtén el
desfase en grados.
Teniendo en cuenta que hemos tomado el origen de tiempos de tal forma
que la fase inicial de la señal de entrada al circuito (canal 1)
sea nula, escribe el valor de la fase inicial de la tensión en
bor-nes de la resistencia (canal 2) con su signo correspondiente:
φ2 =
La otra forma de cálculo se realiza a partir de
las figuras de Lissajous. Éstas aparecen en la pantalla del
osciloscopio al representar en el eje de ordenadas la señal del
canal 1 y en el de abscisas la señal del canal 2. Para ello,
teniendo seleccionada la señal del canal 1 en la forma normal,
se presiona la tecla x-y. Aparecerá en pantalla una elipse
inclinada cuya anchura dependerá del valor del desfase entre
ambas señales. Una vez centrada la elipse con los ejes de
referencia, se puede demostrar que el desfase se puede calcular a
partir de la expresión:
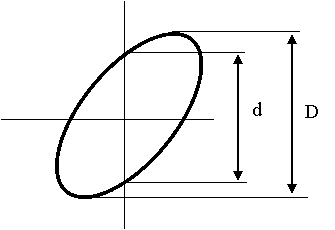
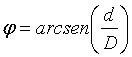
donde D y d son las distancias
señaladas en la
figura.
No podemos conocer el signo del desfase a partir de las figuras de
Lissajous (el signo afectará úni-camente al sentido de
giro del punto en la pantalla, sólo visible a bajas frecuencias).
CUESTIÓN 6. Calcula el desfase de ambas señales a
partir de la figura de Lissajous. Dibuja en el gráfico la figura
de Lissajous visualizada en pantalla y desarrolla claramente el proceso
de cálculo. Obtén el desfase en grados.

Coloca en la siguiente tabla los valores hallados por ambos
métodos:
|
Valor de φ=φ 2-φ1 en grados
|
Método dual
|
|
Fig Lissajous
|
|
CUESTIÓN 7
. Conocidos todos los parámetros que afectan al comportamiento
de nuestro circuito, ahora podremos escribir de forma correcta las
expresiones de la tensión de entrada y de la intensi-dad que
circula por el mismo, considerando el origen de tiempos de tal forma
que la fase inicial de la tensión
de entrada sea nula:
La expresión de la tensión de entrada ya la
obtuvimos al completar la cuestión 2 y el valor de la intensidad
será el valor de la d.d.p. en bornes de la resistencia
(señal del canal 2) dividida por el valor de dicha resistencia:
|
Amplitud
|
Pulsación
|
Fase inicial
|
Expresión matemática
|
Tensión de entrada (*)
V
1(t)=V2m cos(ωt+ φ1 )
|
|
|
|
|
d.d.p. en la resistencia
V2(t)=V2m cos(ωt+ φ2 )
|
|
|
|
|
Intensidad
i(t)=I
2mcos(ω t+ φ i )
|
|
|
|
|
R =
|
|
|
|
|
(*)
completar con
los valores de reflejados en la tabla de la cuestión 2.
Una vez tienes las ecuaciones que representan la tensión de
entrada al circuito y la intensidad que lo atraviesa, se pueden
reproducir fácilmente en una hoja de cálculo.
CUESTIÓN 8. El valor del desfase depende tanto de la
frecuencia como de los elementos que con-forman el circuito. Una forma
de visualizar rápidamente los cambios en el valor de φ es a partir de las
figuras de Lissajous. Entonces, con la figura de Lissajous en la
pantalla modifica considerable-mente el valor de la frecuencia de la
señal de entrada, llegando a valores a valores muy superiores a
los 800 Hz:
¿Qué sucede con las figuras de Lissajous al aumentar la
frecuencia?
En el circuito Resistencia-Condensador que estamos estudiando
¿Qué sucede con el valor del desfa-se al aumentar la
frecuencia?
CUESTIÓN 9. haciendo uso del método que quieras,
mide el valor del desfase a 200, 800 y 25000 Hz y completa la tabla
siguiente:
|
200 Hz
|
800 Hz (*)
|
25000 Hz
|
Valor de φ en grados
|
|
|
|
(*) Valor
calculado con anterioridad.
CUESTIÓN
10. Estudiaremos también como se modifica el desfase al
variar la resistencia del circuito. Para ello mediremos el desfase para
tres resistencias diferentes, de 22 Ω, 120 Ω y 1500 Ω a una frecuencia
de 800 Hz. Completa la tabla siguiente:
|
22 Ω
|
120 Ω
(*)
|
1500 Ω
|
Valor de φ en grados
|
|
|
|
(*) Valor
calculado con anterioridad.
¿Qué
sucede con el desfase al aumentar la resistencia (o el carácter
resistivo)
del circuito? ¿Qué crees que sucedería si en vez
de
una resistencia y un condensador, únicamente tuviésemos
una
resistencia en el circuito?
Laboratorio virtual.
NOTA:
Para poder ejecutar el laboratorio
virtual y el osciloscopio
virtual, es necesario tener instalado en el navegador el plug-in
Java SE Runtime Environment. Recomendamos el uso de la versión
6: Java Runtime Environment (JRE) 6,
aunque también funciona con la versión 1.4.2.
Dicho
software lo puedes descargar desde la web de Sun
Microsystems, Inc .
Para que el
laboratorio virtual se comunique correctamente con el
osciloscopio virtual es necesario habilitar los permisos en el fichero java.policy
del plugin de Java.
Puedes encontrar dicho archivo en:
- C:\Archivos de
programa\Java\jreX.Y\lib\security en Windows
- /usr/java/jreX.Y/lib/security/
o /opt/jreX.Y/lib/security/ en Linux
- ...
Siendo X.Y la
versión del jre que tengas instalada en tu ordenador. La
localización exacta del fichero puede depender de la
versión que tengas instalada.
En dicho fichero hay que añadir, al final del todo, la linea:
grant {
permission java.security.AllPermission; };
En algunos navegadores (por ejemplo Internet Explorer), en la barra de
información
situada debajo de la direcciones, puede aparecer el mensaje "Para
ayudar
a proteger su seguridad, Internet Explorer impidió que este
archivo
mostrara contenido activo que podría tener acceso al equipo.
Haga
clic aquí para ver opciones…" resaltado en color amarillo. En
este
caso, para ejecutar el programa es necesario pulsar con el ratón
en
dicha barra, y seleccionar la opción "Permitir contenido
bloqueado...".
El programa
laboratorio virtual funciona con los navegadores más utilizados
en Windows y Linux. Para obtener más
información
acerca de los diferentes navegadores y sistemas operativos compatibles
con
el programa pincha en el enlace compatibilidades.