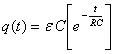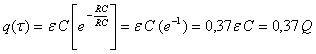PRÁCTICA
3
FENÓMENOS TRANSITORIOS. LA CARGA Y DESCARGA DE CONDENSADORES.
Introducción
1. Objetivos
2. Material
3. Transitorios en fenómenos
físicos
4. El condensador
4.1. Condensador
4.2. Condensador plano
4.3. Condensador
cilíndrico: cable coaxial
4.4. Dieléctricos en
los condensadores
4.5. Asociación de
condensadores
Asociación
en paralelo
Asociación
en serie
5. Régimen transitorio de un circuito RC. Procesos de carga y descarga
del condensador
5.1. Carga
5.2. Descarga
5.3. Método de
medida
6. Experiencia a desarrollar
6.1. Medida de la constante
de tiempo en la carga y descarga de condensadores: evaluación
del sistema de medida
6.2. Determinación de
valores de capacidades y resistencias
6.3.
Comprobación de las leyes de asociación de condensadores
7. Laboratorio virtual
INTRODUCCIÓN
En el enlace “osciloscopio”
se explica las nociones básicas sobre el funcionamiento interno
del osciloscopio, y se da instrucciones sobre la utilización del
osciloscopio analógico Hameg. Para la realización de
esta práctica
es necesario también conocer el funcionamiento del
generador de funciones .
En esta
práctica vamos a realizar el circuito de carga y descarga de un
condensador mediante el programa
laboratorio virtual . Puedes encontrar información sobre
el funcionamiento del programa en el enlace "ayuda laboratorio
virtual". Las medidas de diferencia de potencial se realizan
mediante el
osciloscopio virtual. En
este enlace podéis encontrar un manual para aprender su
funcionamiento.
1. OBJETIVOS
- Estudiar los fenómenos transitorios, y la constante de
tiempo
como parámetro. En particular, estudiar la carga y descarga del
condensador.
- Practicar el diseño de experimentos.
- Utilización de equipos: osciloscopio virtual
- Errores en medidas de tiempo.
- Ajustes por mínimos cuadrados y función Solver de
EXCEL.
2. MATERIAL
- Generador de funciones.
- Osciloscopio virtual.
- Tres condensadores: 2,2 μF, 4,4 μF y 6,8 μF.
- Tres resistencias: 220 Ω, 1kΩ, 100 kΩ y resistencia
incógnita.
- Placa de conexiones.
- Cables.
- Ordenador con hoja de cálculo.
3. TRANSITORIOS EN FENÓMENOS FÍSICOS
Los procesos transitorios aparecen siempre que un sistema
físico
sufre una alteración súbita en su estado de
funcionamiento
“normal”, al que se denomina régimen permanente de
funcionamiento.
Cuando se le aparta de este estado, el sistema tarda un tiempo en
adecuarse
a la nueva situación, tiempo durante el cual se produce
variaciones
más o menos “rápidas” de las magnitudes del sistema,
hasta
llegar de nuevo a una situación de equilibrio adaptada a las
nuevas
condiciones. Estos procesos que ocurren entre el estado de
régimen
permanente inicial y el final se conocen como procesos transitorios, y
en
Física e Ingeniería tienen una importancia capital, ya
que
en muchas ocasiones, durante los transitorios algunas magnitudes
físicas
alcanzan valores mucho mayores que los que se producen durante el
régimen
permanente, y ello debe ser tenido en cuenta a la hora de
diseñar
el sistema.
Un típico ejemplo de un proceso transitorio es el que se
produce
al hacer vibrar una cuerda mediante una pulsación (por ejemplo
de
una guitarra). Inicialmente, la cuerda estaba en equilibrio, y
finalmente
también, pero entre ambos estados, la cuerda vibra con una
amplitud
que va disminuyendo con el tiempo. Dicho proceso vibratorio es el
proceso
transitorio.
En un circuito eléctrico, el fenómeno por el cual los
electrones
se ponen en movimiento también da lugar a procesos transitorios.
En
un circuito en el que no hay ninguna tensión eléctrica
aplicada
y, por tanto, no hay corriente eléctrica, si en un momento dado
se
aplica una tensión al circuito, hasta que se alcanza la
corriente
estable de funcionamiento del circuito (corriente nominal) se produce
corrientes
que pueden ser mayores que la nominal. Es por ello por lo que cualquier
informático
sabe que no es recomendable conectar o desconectar ningún
dispositivo
a un ordenador mientras éste se encuentre en funcionamiento, o
también
sabe que una repentina bajada en la tensión de la red
eléctrica
(o su restablecimiento) puede tener efectos nefastos sobre la fuente de
alimentación.
Además, estas variaciones pueden ser tan rápidas que un
fusible
convencional no proteja el aparato, y a pesar de su presencia, se puede
producir
desperfectos. Para evitarlos es necesario instalar otros dispositivos
(interruptores
diferenciales) que reaccionan frente a la rapidez de variación
de
la corriente, y no frente a valores absolutos de ésta.

Figura 1: Ejemplo de un transitorio de corriente al conectar un
circuito con una resistencia eléctrica, un efecto de capacidad y
efectos de autoinducción. La intensidad pasa por valores
máximos en un proceso cuya duración depende de los tres
elementos indicados.
En la práctica presente, se va a estudiar el proceso
transitorio
que se produce desde el instante en que a un circuito RC se le aplica
una
tensión, hasta que se alcanza el régimen de
funcionamiento
permanente del circuito. Se estudiará los factores que
intervienen
en el tiempo de duración del proceso.
4. EL CONDENSADOR
4.1. CONDENSADOR
Es un sistema de dos conductores (armaduras) que se ejercen
influencia
total. Sirven para almacenar cargas eléctricas y energía.
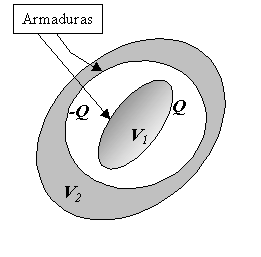
Figura 2: Esquema de un condensador.

Figura 3: Fotografía de un conjunto de condensadores
|

Figura 4: Fotografía de un condensador electrolítico
|
El proceso de carga de un condensador supone situarlo en un circuito
eléctrico,
con cada armadura conectada a un potencial electrostático
diferente.
Como consecuencia de esto habrá un desplazamiento de cargas de
una
de las armaduras a la otra, hasta que la diferencia de potencial
aplicada
entre ellas se corresponda con la creada por las cargas situadas sobre
las
superficies de las armaduras entre las que existe la influencia total.
La capacidad de un condensador se define como la relación
entre
la carga desplazada de una a otra armadura y la diferencia de potencial
entre
ellas
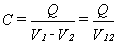
En los circuitos eléctricos la representación
gráfica
de los condensadores es la del dibujo:

La mayor parte de los condensadores tienen indicada su capacidad en
el
exterior, generalmente con capacidades entre pico y microfaradios, y su
conexión
a los circuitos no tiene ningún requisito especial, excepto en
el
caso de los condensadores electrolíticos. En estos su gran
capacidad,
del orden de milifaradios, está basada en los compuestos
químicos
resultantes de una reacción electrolítica, y la polaridad
del
condensador es fundamental. En la fotografía de la figura 4 se
puede
apreciar un signo + en uno de sus extremos que indica la
conexión
a la armadura que debe estar situada a mayor potencial en el circuito
eléctrico.
4.2. CONDENSADOR PLANO

Figura 5: Esquema de un condensador plano.
El condensador plano tiene las armaduras con sus superficies planas
y
paralelas. Normalmente la separación entre las armaduras d
será
muy pequeña comparada con las dimensiones de la superficie de
las
armaduras, con lo que se podrá suponer unas condiciones de
distribución
de carga uniforme para toda la superficie, despreciando el efecto de
los
bordes, con una densidad superficial de carga 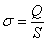 , donde S es el
área
de la superficie. Bajo estas condiciones las superficies
equipotenciales
en el espacio entre las armaduras serán planos paralelos a las
armaduras,
y el campo eléctrico será normal a ellas, en el sentido
de
la armadura con carga positiva a la negativa, y uniforme. La
expresión
que se obtiene para la capacidad del condensador plano es:
, donde S es el
área
de la superficie. Bajo estas condiciones las superficies
equipotenciales
en el espacio entre las armaduras serán planos paralelos a las
armaduras,
y el campo eléctrico será normal a ellas, en el sentido
de
la armadura con carga positiva a la negativa, y uniforme. La
expresión
que se obtiene para la capacidad del condensador plano es:
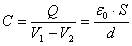
La mayor parte de los condensadores utilizados en los circuitos
electrónicos
son paralelos. Algunos, como el de la foto, tienen una apariencia
externa
cilíndrica, pero en la sección se puede observar como se
trata
de un condensador plano, de armaduras muy finas y separadas por una
película
aislante, enrollado sobre sí mismo para ocupar el mínimo
espacio.

Figura 6: fotografía de un condensador, donde se muestra que se
trata de un condensador plano enrollado sobre sí mismo.
4.3. CONDENSADOR CILÍNDRICO: CABLE COAXIAL

Figura 7: Cable coaxial.
Un caso importante de condensador en un laboratorio de
electricidad/electrónica
son los cables coaxiales. La geometría de los conductores es la
de
condensador cilíndrico, y su capacidad viene dada en
función
de la longitud del cable L, y de los radios interno y externo R1
y R2
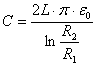
4.4. DIELÉCTRICOS EN LOS CONDENSADORES
Normalmente el espacio comprendido entre las dos armaduras del
condensador
está relleno de un aislante (dieléctrico) que mantiene la
distancia
entre las armaduras, y, al mismo tiempo, aumenta la capacidad del
condensador.
El efecto del campo eléctrico sobre los aislantes, la
polarización,
supone una disminución en el valor del campo y la diferencia de
potencial
entre las armaduras. Por lo tanto, al someter un condensador con
dieléctrico
a una diferencia de potencial la carga almacenada es mayor que la que
se
tendría en el mismo condensador sin el aislante. La capacidad
aumenta
en un factor constante que depende del material utilizado como
aislante,
y que se denomina permitividad dieléctrica relativa del material
εr.
De esta forma la capacidad del condensador será: C =
C0·εr
, siendo C0 la capacidad del mismo condensador sin
dieléctrico.
A partir de la expresión de la capacidad del condensador
plano
con dieléctrico se puede entender los criterios utilizados para
conseguir
capacidades altas:

Puesto que el valor de la permitividad dieléctrica relativa
está
limitado dentro de los valores que se indica en la tabla 1, aumentar la
superficie
de las armaduras o disminuir el espesor de la capa de
dieléctrico,
y por tanto la distancia entre armaduras, son los parámetros
sobre
los que se actúa para mejorar la capacidad.
Material
|
εr |
Aceite
Agua a 20ºC
Aire
Baquelita
Mica
Neopreno
Papel
Parafina
Plexiglás
Porcelana
Vidrio pyrex
|
2,24
80
1,0006
4,9
5,4
6,9
3,7
2,3
3,4
7
5,6
|
Tabla 1: Permitividad dieléctrica relativa de diversos
materiales.
4.5. ASOCIACIÓN DE CONDENSADORES
Se define la capacidad equivalente de una asociación de
condensadores
a la capacidad de un único condensador tal que al aplicar la
misma
ddp almacene la misma carga.
Existen dos disposiciones básicas
en
las asociaciones de condensadores: asociación en paralelo y en
serie.
Buena parte de las asociaciones de condensadores podrán
reducirse
a combinaciones de serie y paralelo. Mediante asociaciones de
condensadores
se puede conseguir valores de capacidad equivalentes que no se
podría
obtener directamente con condensadores comerciales.
Asociación en paralelo:
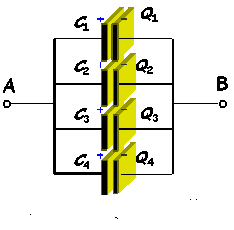
Figura 8: Esquema de la asociación en paralelo de condensadores.
|

Figura 9: Asociación de condensadores en paralelo utilizada en
los circuitos de sintonización de radio.
|
Todos los condensadores están conectados entre un par de
nudos,
y por lo tanto tendrán la misma diferencia de potencial entre
sus
armaduras. La carga total intercambiada entre las armaduras será
la
suma de la carga de cada condensador.
El condensador equivalente almacenará la misma carga al ser
sometido
a la misma diferencia de potencial, y su capacidad será:
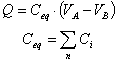
En la figura 9 aparece una asociación de condensadores en
paralelo
utilizada en los circuitos de sintonización de radio. Las
armaduras
pueden girar con el mando del dial, introduciéndose más o
menos
en el resto de armaduras, aumentando así la superficie de
influencia
de los condensadores, y por lo tanto su capacidad. La capacidad total
del
conjunto será la suma de las capacidades de todos ellos, en la
fotografía
son 25.
Asociación en serie:

Figura 10: Esquema de la asociación en serie de condensadores.
En esta disposición la segunda armadura del primer
condensador
está conectada con la primera del segundo, y de igual manera se
conecta
el resto. De esta forma la segunda armadura del primero y la primera
del
segundo forman un conjunto aislado y equipotencial, al igual que el
resto
de conjuntos equivalentes. El intercambio de cargas se verifica
únicamente
entre la primera y la última armadura, pero todos los
condensadores,
por la influencia entre las armaduras, aparecen cargados con la misma
carga.
La capacidad del condensador equivalente es:
/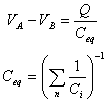
5. RÉGIMEN TRANSITORIO DE UN CIRCUITO RC. PROCESOS DE CARGA
Y
DESCARGA DEL CONDENSADOR
Un fenómeno importante dentro del estudio de los circuitos
eléctricos
son los procesos transitorios conducentes a condiciones de
régimen
permanente. Por ejemplo, desde el momento en que se conecta los
generadores
a los circuitos hasta que se llega a las condiciones de régimen
permanente,
valores constantes de intensidades de corriente, diferencias de
potencial,
cargas..., transcurre un cierto tiempo en el que las diferentes
magnitudes
varían hasta llegar a estabilizarse en el valor en corriente
continua.
La presencia en los circuitos de condensadores, bobinas, o la propia
autoinducción
de los circuitos, provocan la aparición de estos
regímenes
transitorios.
Se va a estudiar el caso del circuito RC, formado por un condensador
de
capacidad C, una resistencia R conectada en serie, y un
generador de
fuerza
electromotriz ε. El circuito se cierra mediante un interruptor, tal
como
se indica en la figura 11.

Figura 11: Circuito RC para
la carga de un condensador.
5.1. CARGA
Inicialmente el condensador está descargado. Cuando se cierra
el
interruptor se inicia el proceso de carga, que supone un movimiento de
cargas
entre sus armaduras a lo largo del circuito. La fuerza electromotriz
del
generador siempre será la suma de la diferencia de potencial en
el
condensador y en la resistencia,
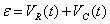
Al finalizar el proceso de carga el condensador actuará como
un
circuito abierto, y la intensidad de corriente será cero. Por
tanto
la condición
inicial del circuito es que el condensador
está
descargado (q=0), y la final
que el movimiento de cargas desaparece
(i=0),
y por lo tanto la diferencia de potencial en el condensador será
igual
a la f.e.m. del generador. Se llamará Q a la carga final que
adquiere
el condensador.
La intensidad de corriente que circula por el circuito es la
correspondiente
al proceso de carga del condensador: si, a partir de un instante t, en
un
dt la carga del condensador q(t)
aumenta un dq(t), la
intensidad que
circula
será i(t)=dq(t)/dt ,
es decir, la carga que se mueve entre las
armaduras
del condensador por unidad de tiempo. Por otro lado, la capacidad del
condensador
siempre se mantendrá como relación constante entre carga
y
diferencia de potencial: C=q(t)/Vc(t).
Si todo lo anterior se utiliza en la ecuación de las
diferencias
de potencial:
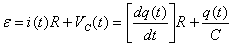
Ecuación diferencial que se puede integrar para obtener la
expresión
de la carga del condensador en función del tiempo, aplicando la
condición
inicial según la cual en el instante inicial el condensador
está
descargado:
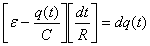 -->
--> 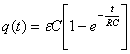
La carga sigue una ley exponencial, va aumentando desde carga cero a
la
carga máxima Q=ε·C
en tiempo infinito. La idea de
tiempo
infinito
se puede matizar mediante la constante de tiempo, τ, que se define como τ=RC,
y tiene dimensiones de tiempo. Si se hace que el tiempo de carga tenga
por
valor la constante de tiempo:
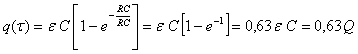
La constante de tiempo es el tiempo para el que el condensador se ha
cargado
con el 63% de su carga total. Puede dar una idea de la velocidad del
proceso
de carga, y de como controlarlo: un condensador de 1 µF conectado
a
una resistencia de 100 Ω tardará 0,0001segundos en llegar al
63%
de
carga, mientras que conectado a una resistencia de 100 kΩ
tardaría
0,1 segundos, el proceso sería mucho más lento.
En el laboratorio difícilmente se puede medir de forma
directa
la carga del condensador, pero sí que se puede medir la
diferencia
de potencial entre sus armaduras, que también seguirá la
misma
ley exponencial:
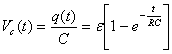
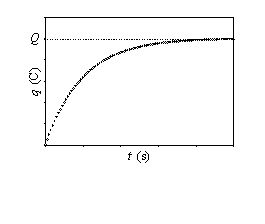
Figura 12: Representación gráfica de la carga del
condensador en función del tiempo.
|

Figura 13: Interpretación de la constante de tiempo τ en el
circuito de carga.
|
Los datos experimentales que se recoja serán diferencias de
potencial
en función del tiempo de carga. A partir de ellos se puede
determinar
la constante de tiempo de dos formas diferentes:
a) Observando el valor máximo de la diferencia de potencial y
determinando
el tiempo para el que la diferencia de potencial en el condensador es
el
63% de la máxima.
b) Realizando un ajuste de los datos experimentales a la
ecuación
anterior, determinando de esta forma los parámetros del ajuste,
ε y τ.
5.2. DESCARGA
Una vez cargado el condensador, el proceso de descarga consiste en
cortocircuitar
el conjunto resistencia-condensador (figura 14). De esta forma las
cargas
de las armaduras podrán neutralizarse, se moverán de una
a
la otra produciendo una corriente eléctrica que se
anulará
cuando se descargue por completo el condensador.
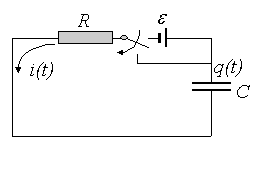
Figura 14: Circuito de descarga de un condensador.
Al iniciar el proceso el condensador estará cargado con carga
Q,
la que haya adquirido durante el proceso inicial, y al finalizar la
carga
será cero. Por otro lado, durante el proceso de descarga se
seguirá
manteniendo la misma capacidad característica del condensador,
relación
entre la carga y la diferencia de potencial entre armaduras. La
ecuación
del circuito ahora será:
0=i(t)R+VC(t)
Durante la descarga, la carga del condensador disminuye, y esa
disminución
es igual a la carga que se mueve por el circuito: en un instante t la
carga
del condensador q(t)
disminuye en un dq(t) durante
un tiempo dt
(q(t)--> q(t+dt)=q(t)-dq(t)).
Ese -d(q) es la carga que se
mueve por el circuito en el tiempo dt,
por
lo
que la intensidad será i(t)=
-dq(t)/dt. Se debe considerar
también
que en el proceso de descarga la corriente circula en sentido contrario
al
que tenía durante la carga:
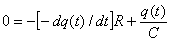 -->
--> 
Integrando la ecuación diferencial, y teniendo en cuenta el
valor
de la carga inicial del condensador (Q), se obtiene la expresión
de
la carga en función del tiempo:
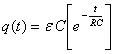
El proceso de descarga sigue una ley exponencial decreciente. El
significado
de la constante de tiempo es semejante al que tenía en la carga.
El
valor de la carga del condensador en un tiempo de descarga igual a la
constante
de tiempo es:
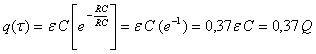
Es decir que a un tiempo igual a la constante de tiempo el
condensador
se ha descargado hasta un valor igual al 37% de la carga inicial. La
forma
en la que se estudia el proceso de descarga, y se determina la
constante
de tiempo, es la misma que en proceso de carga, es decir, midiendo la
diferencia
de potencial en el condensador:

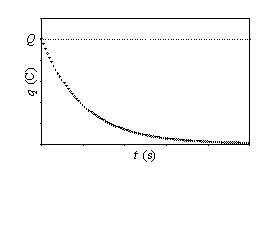
Figura 15: Representación gráfica de la descarga del
condensador en función del tiempo.
|
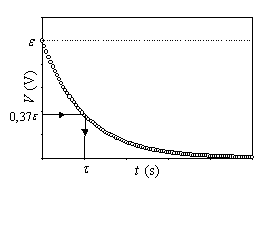
Figura 16: Interpretación de la constante de tiempo τ en el
circuito de descarga.
|
5.3. MÉTODO DE MEDIDA
Medida de constantes de tiempo
En las medidas de constantes de tiempo siempre aparece el problema
de
la rapidez del proceso transitorio que se estudia. Los métodos
de
medida tendrán su limitación fundamental en este factor,
ya
que habrán sistemas de medida muy precisos, pero con medidas
lentas,
que no permitirán el estudio de procesos transitorios
rápidos,
y por otro lado sistemas de medida de muestreo muy rápido y no
demasiada
precisión, que, a pesar de esto, serán los únicos
que
permitirán el estudio de transitorios de muy corta
duración.
A continuación se presenta tres posibles sistemas de medida
para
los procesos de carga y descarga del condensador cuya aplicación
dependerá
de lo anteriormente comentado.
Medidas directas con cronómetro y multímetro
La forma más inmediata de medir el proceso de carga y
descarga
de un condensador, igual que cualquier transitorio, es utilizando un
cronómetro
y un aparato que mida la magnitud que se desea estudiar.
Medidas con la tarjeta de adquisición de datos.
Los procesos de carga y descarga de un condensador se puede medir
mediante
un ordenador, a través de una tarjeta conversora que es capaz de
hacer
dos tareas simultáneamente:
a) Puede convertir tensiones analógicas que llegan a la
tarjeta,
en señales digitales, capaces de ser procesadas por el ordenador.
b) Puede proporcionar una tensión en una de sus salidas,
según
el valor de tensión indicado por el ordenador.
Medidas con el osciloscopio
Una posible forma de medir las constantes de tiempo de
fenómenos
transitorios en circuitos eléctricos es la utilización de
los
generadores de funciones suministrando una señal en
escalón.
La duración de los tramos del escalón, que se controla
mediante
la frecuencia del generador, debe ser superior al tiempo de
duración
del transitorio. De esta manera se estaría realizando sucesivos
procesos
de carga y descarga del circuito. Con el osciloscopio se mide la
evolución
temporal de la variable a estudiar, en este caso la diferencia de
potencial
en el condensador V, que es
proporcional a la carga que almacena: Q=CV.
En el generador de funciones se puede seleccionar la función
escalón.
La frecuencia deberá ser la suficiente para que suponga que se
haya
establecido el régimen estacionario tras el transitorio. Esto se
puede
observar en la pantalla del osciloscopio.

Figura 17: Indicador de la función escalón en el
generador de funciones.
En el osciloscopio virtual puedes visualizar en los dos canales la
diferencia
de potencial a la salida del generador de funciones y en el
condensador.
La imagen que obtendrás será semejante a la de la figura
18
si se llega de forma completa a la carga y descarga del condensador.
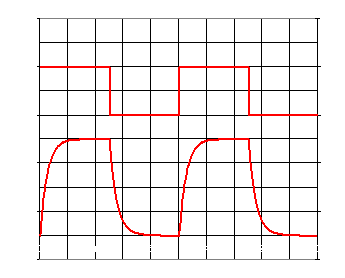
Figura 18: Tensión en bornes del generador y del condensador.
En la pantalla del osciloscopio, se puede medir el valor máximo
de
la diferencia de potencial en el condensador Vmáx, y,
por lo
tanto,
podrás calcular el valor 0,63·Vmáx, que
es el que
se
alcanza durante la carga en un tiempo igual a la constante de tiempo,
pudiendo
medir de esta forma dicha constante de tiempo.
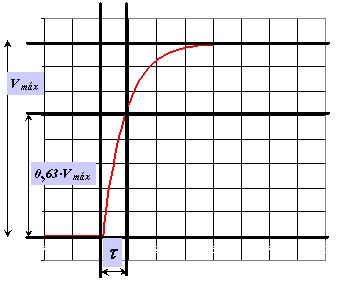
Figura 19: Medida de la constante de tiempo.
6. EXPERIENCIA A DESARROLLAR
La primera parte de la experiencia se centra en analizar el proceso
de
carga y descarga del condensador como método de
determinación
indirecta de valores de capacidades y resistencias. En la segunda se
utiliza
el método para comprobar las leyes de asociación de
condensadores.
6.1. Medida de la constante de tiempo en
la carga y descarga de
condensadores: evaluación del sistema de medida.
La constante de tiempo del circuito depende de los valores de
resistencia
y capacidad, por lo que antes de realizar el proceso de carga o
descarga
has de conocer, aunque sea de forma aproximada, el valor de la
constante
de tiempo del circuito. Calcula la
constante
de tiempo teórica del circuito, τteórica, que
viene
dada
por
los valores de la resistencia R
y capacidad C utilizada, y
completa así la tercera columna de la tabla.
Mide mediante el osciloscopio la constante de tiempo en el proceso de
carga, τcarga, y en el de descarga, τdescarga.
Observa que debes variar la frecuencia del generador de funciones en
función del valor de la constante de tiempo del circuito, para
poder observar adecuadamente tanto el proceso de carga como el de
descarga del condensador. Anota la frecuencia utilizada en la
última columna.
| Valores nominales |
Experimental
|
frecuencia
del generador |
| R |
C |
τteórica |
τcarga |
τdescarga |
| 220 Ω |
2,2 μF |
|
|
|
|
| 220 Ω |
4,4 μF |
|
|
|
|
| 220 Ω |
6,8 μF |
|
|
|
|
| 1kΩ |
2,2 μF |
|
|
|
|
| 1kΩ |
4,4 μF |
|
|
|
|
| 1kΩ |
6,8 μF |
|
|
|
|
| 100 kΩ |
2,2 μF |
|
|
|
|
| 100 kΩ |
4,4 μF |
|
|
|
|
| 100 kΩ |
6,8 μF |
|
|
|
|
Observa que en algunos casos la constante de tiempo NO se
podrá
medir dadas las limitaciones del método de medida. ¿para
qué valores de resistencia y capacidad no es posible medir la
constante de tiempo? ¿por qué?
6.2. Determinación de valores de
capacidades y resistencias.
Una vez que tengas claro las limitaciones del método de medida
según
los valores de R y C, realiza el proceso
carga/descarga con la
finalidad
de determinar valores de capacidades y resistencias, ya sea conociendo
R
y tratando de determinar C o
a la inversa.
a. Mide con el
multímetro la resistencia de 1kΩ.
Valor nominal
|
Valor
experimental
|
| 1kΩ |
|
Determina la
capacidad del condensador de 6,8 μF mediante carga/descarga
de
circuito
RC conociendo el valor de R medido con el óhmetro.
Competa la tabla siguiente.
| Valores nominales |
Valores experimentales |
frecuencia
del generador |
| R |
C |
τcarga
|
τdescarga |
C
|
| 1kΩ |
6,8 μF |
|
|
|
|
b. Determina el valor de la
resistencia incógnita mediante
carga/descarga de circuito RC
conociendo
el valor de C (para ello
utiliza el condensador de 6,8 μF que has medido en el apartado
anterior). Completa la tabla siguiente.
| Valores nominales |
Valores experimentales |
frecuencia
del generador |
| R |
C |
τcarga
|
τdescarga |
R |
| resistencia
incógnita |
6,8 μF |
|
|
|
|
Puedes repetir los dos apartados con diferentes condensadores y
resistencias
para comprobar la validez del método y comparar los resultados
obtenidos.
6.3. Comprobación de las
leyes de asociación de
condensadores.
a. Capacidad equivalente de
condensadores en serie:
i. Diseña un
circuito con el que puedas comprobar la ley de
asociación
de condensadores en serie para dos condensadores de capacidad
diferente.
ii. Determina la
capacidad equivalente de los dos condensadores
mediante
la constante de tiempo en la carga/descarga.
iii. Analiza y discute el
resultado experimental. Compáralo con el resultado
teórico esperado.
| Valores nominales |
Valores experimentales |
frecuencia
del generador |
C1
|
C2 |
Ceq
|
τcarga
|
τdescarga |
Ceq |
|
|
|
|
|
|
|
b. Capacidad equivalente de
condensadores en paralelo:
i. Diseña un
circuito con el que puedas comprobar la ley de
asociación de condensadores en paralelo para dos condensadores
de
capacidad diferente.
ii. Determina la capacidad
equivalente de los tres condensadores
mediante
la constante de tiempo en la carga/descarga.
iii. Analiza y discute el
resultado experimental. Compáralo con el resultado
teórico esperado.
| Valores nominales |
Valores experimentales |
frecuencia
del generador |
C1
|
C2 |
Ceq
|
τcarga
|
τdescarga |
Ceq |
|
|
|
|
|
|
|
c. Capacidad de asociaciones
mixtas serie/paralelo:
i. Diseña un
circuito con dos condensadores (C1
y C2) en paralelo
en
serie con un tercer condensador (C3).
ii. Determina la
capacidad equivalente de los tres condensadores
mediante la constante de tiempo en la carga/descarga.
iii. Analiza y discute el
resultado experimental. Compáralo con el resultado
teórico esperado.
| Valores nominales |
Valores experimentales |
frecuencia
del generador |
C1
|
C2 |
C3 |
Ceq
|
τcarga
|
τdescarga |
Ceq |
|
|
|
|
|
|
|
|
d. Determinación de
la capacidad de asociaciones de
condensadores
en las que la capacidad equivalente no se pueda determinar por
combinaciones
serie paralelo:
i. Determina la capacidad
equivalente de la asociación
de cinco condensadores de la figura 20 mediante la constante de tiempo
en
la carga/descarga.
Observa que no podrás calcular la capacidad equivalente
como combinaciones serie paralelo.
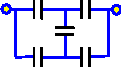
Figura 20: Asociación de cinco condensadores.
ii. Analiza y discute el
resultado experimental.
| Valores nominales |
Valores experimentales |
frecuencia
del generador |
C1
|
C2 |
C3 |
C4 |
C5
|
τcarga
|
τdescarga |
Ceq |
|
|
|
|
|
|
|
|
|
7. LABORATORIO VIRTUAL
NOTA:
Para poder ejecutar el laboratorio
virtual y el osciloscopio
virtual, es necesario tener instalado en el navegador el plug-in
Java SE Runtime Environment. Recomendamos el uso de la versión
6: Java Runtime Environment (JRE) 6,
aunque también funciona con la versión 1.4.2.
Dicho
software lo puedes descargar desde la web de Sun
Microsystems, Inc .
Para que el
laboratorio virtual se comunique correctamente con el
osciloscopio virtual es necesario habilitar los permisos en el fichero java.policy
del plugin de Java.
Puedes encontrar dicho archivo en:
- C:\Archivos de
programa\Java\jreX.Y\lib\security en Windows
- /usr/java/jreX.Y/lib/security/
o /opt/jreX.Y/lib/security/ en Linux
- ...
Siendo X.Y la
versión del jre que tengas instalada en tu ordenador. La
localización exacta del fichero puede depender de la
versión que tengas instalada.
En dicho fichero hay que añadir, al final del todo, la linea:
grant {
permission java.security.AllPermission; };
En algunos navegadores (por ejemplo Internet Explorer), en la barra de
información
situada debajo de la direcciones, puede aparecer el mensaje "Para
ayudar
a proteger su seguridad, Internet Explorer impidió que este
archivo
mostrara contenido activo que podría tener acceso al equipo.
Haga
clic aquí para ver opciones…" resaltado en color amarillo. En
este
caso, para ejecutar el programa es necesario pulsar con el ratón
en
dicha barra, y seleccionar la opción "Permitir contenido
bloqueado...".
El programa
laboratorio virtual funciona con los navegadores más utilizados
en Windows y Linux. Para obtener más
información
acerca de los diferentes navegadores y sistemas operativos compatibles
con
el programa pincha en el enlace compatibilidades.




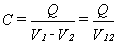


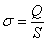 , donde S es el
área
de la superficie. Bajo estas condiciones las superficies
equipotenciales
en el espacio entre las armaduras serán planos paralelos a las
armaduras,
y el campo eléctrico será normal a ellas, en el sentido
de
la armadura con carga positiva a la negativa, y uniforme. La
expresión
que se obtiene para la capacidad del condensador plano es:
, donde S es el
área
de la superficie. Bajo estas condiciones las superficies
equipotenciales
en el espacio entre las armaduras serán planos paralelos a las
armaduras,
y el campo eléctrico será normal a ellas, en el sentido
de
la armadura con carga positiva a la negativa, y uniforme. La
expresión
que se obtiene para la capacidad del condensador plano es: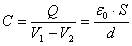


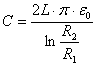



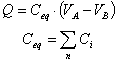

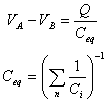

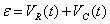
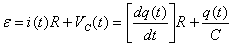
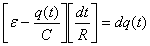 -->
--> 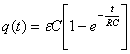
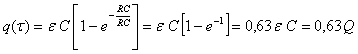
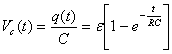



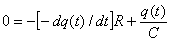 -->
-->