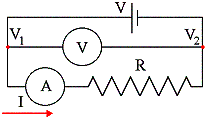
Hemos visto que para medir resistencias podemos emplear el óhmmetro. Pero para medir resistencias se puede diseñar un dispositivo que permita medir simultáneamente la intensidad que atraviesa la resistencia y la diferencia de potencial aplicada, haciendo uso de un amperímetro y de un voltímetro respectivamente, para, a continuación, aplicar la ley de Ohm. Existen dos posibles disposiciones para colocar los aparatos de medida que se denominan montaje largo y montaje corto. En esta primera práctica se analizará el montaje largo.

En este dispositivo se colocará la resistencia a medir en serie con el amperímetro y el conjunto se conectará a una fuente de tensión. De esta forma el amperímetro mide la intensidad que circula por la resistencia. Con el voltímetro se medirá la diferencia de potencial que aporta la fuente al circuito:
De esta forma se puede conocer el valor de la resistencia sin más que aplicar la ley de Ohm: R=V/I.
En el montaje largo utilizaremos como voltímetro un aparato analógico y como amperímetro el aparato digital que nos indique el profesor o profesora. Fijaremos la tensión de la fuente en 4,5 V. Para lo cual, antes de montar el circuito mediremos con el voltímetro la tensión de la fuente y ajustaremos el valor a los 4,5 V indicados.
CUESTIÓN 1: Identifica cada una de las resistencia que aparecen en la tabla con el código de colores y mídela con el óhmmetro. Realiza el montaje largo para medir las resistencias, y completa la tabla:
|
Rnominal (Ω) |
Medida de resistencias Montaje largo |
Medida óhmmetro |
||
|
V |
|
R=V/I |
R |
|
|
560 |
|
|
|
|
|
1500 |
|
|
|
|
|
3300 |
|
|
|
|
|
6800 |
|
|
|
|
|
12000 |
|
|
|
|
|
15000 |
|
|
|
|
|
22000 |
|
|
|
|
Nota: escribe las medidas con todos los decimales y no olvides tomar nota de la marca y modelo del aparato.
Podemos observar que las medidas realizadas difieren en ambos sistemas de medida y del valor dado por el fabricante. Es más, en el código de colores, el último valor se corresponde con la tolerancia con que ha sido fabricada la resistencia. Es decir, el valor que nos da el fabricante (RN) es el punto medio de un intervalo de valores (RN-ΔRN, RN+ΔRN) dentro del cual se encuentra el valor verdadero de la resistencia. Cuanto más pequeño es este intervalo con más precisión está fabricada la resistencia. El último color del código de colores nos permite conocer ΔR.
Cuando realizamos una medida sucede algo parecido: no podemos conocer el valor exacto de la misma, sino que siempre tendremos un margen de incertidumbre en torno al valor que supongamos como bueno. Esto quiere decir que un valor medido experimentalmente debe venir acompañado por su incertidumbre de la forma R±ΔR, indicativo de que el valor medido se encuentra en el intervalo (R-ΔR, R+ΔR), siendo ΔR, la incertidumbre con que se ha realizado la medida. Una medida será más precisa cuanto más pequeña sea su incertidumbre.
En el tema de "Teoría de errores” se explica con más detalle el concepto de error o incertidumbre asociado a una medida, así como la forma de estimarlo.
El origen de la falta de precisión en las medidas lo encontramos en factores aleatorios basados en los límites físicos de los aparatos de medida o en perturbaciones ambientales o del propio sistema de medida, lo que se denominan errores de medida accidentales. Los aparatos electrónicos vienen acompañados por los datos suficientes para poder calcular la incertidumbre de una medida, cuando ésta se realiza en condiciones apropiadas y el aparato está calibrado y sujeto a un proceso adecuado de mantenimiento.
En los APARATOS DIGITALES la incertidumbre se calcula generalmente como la suma del error de precisión (% de la medida) más el error de lectura (n unidades en el último dígito). En la figura se muestra dos ejemplos de cálculo de incertidumbres, para un aparato digital con error de precisión 2%, y error de lectura 1d. En el puesto de trabajo podéis encontrar las tablas de especificaciones técnicas de los multímetros de que disponéis en el laboratorio.
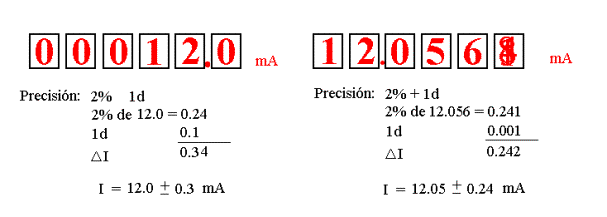
El error de lectura se considerará como el valor correspondiente al valor de n unidades en el último dígito de la pantalla siempre que el valor que aparezca sea de fácil lectura. Podría suceder que por causas ajenas al aparato aparezcan ruidos en la medida y esta vea sus últimos dígitos cambiar continuamente: En este caso ajustaremos el error a la medida que podamos dar por cierta. (ver figura de la derecha). Asimismo trabajaremos siempre en la escala que de mayor precisión. De esta forma, en los ejemplos anteriores, puesto que el error de lectura es de 1d, este error vale 1 unidad en la última cifra que se puede observar en el aparato, es decir, 0,1 mA para el primer caso, y 0,001 mA para el segundo.
Hay aparatos que añaden otros elementos al cálculo del error accidental, como puede ser un porcentaje del fondo de escala (valor máximo que se puede medir en la escala seleccionada) o que consideran el error de lectura dos o más unidades en el último dígito y según escalas. Siempre habrá que seguir las indicaciones marcadas por el fabricante en las especificaciones del aparato.
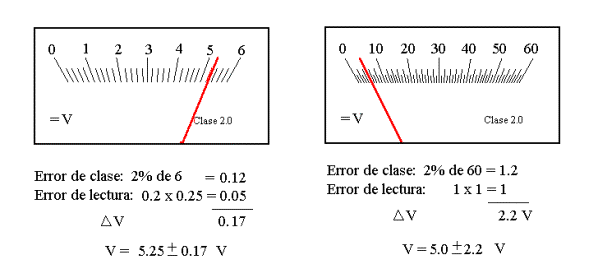
En APARATOS ANALÓGICOS, el error accidental se calcula como suma del error de "clase" (% del fondo de escala) más el error de lectura. La clase del aparato puede ser única para todas las escalas (aunque no siempre sucede así) y suele estar indicada en la misma pantalla. El error de lectura surge de una estimación subjetiva de la capacidad del experimentador para precisar su lectura en la pantalla. Depende de parámetros tales como, la definición de la escala, la limpieza de la pantalla (la placa puede estar desgastada) y el estado anímico o físico del experimentador. En los aparatos de aguja, la lectura se debe realizar siempre desde la perpendicular a la pantalla, para evitar desviaciones debidas al espaciado entre la aguja y la escala (error de paralaje). La figura muestra dos ejemplos de cálculo diferentes.
El cálculo del error de lectura debe supeditarse siempre a la capacidad de lectura del usuario. Así, en los dos ejemplos siguientes el error de lectura será muy diferente al aplicado en el ejemplo anterior con la misma escala.
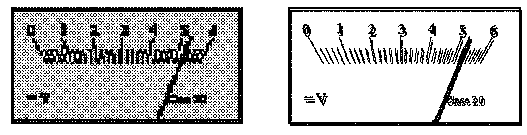
Así podemos conocer la incertidumbre tanto de un aparato digital (suma de las incertidumbres debidas al error de lectura y a la precisión del aparato) como de un aparato de medida analógico (suma de las incertidumbres debidas al error de lectura y al de clase del aparato).
CUESTIÓN 2: Si consideramos únicamente la resistencia de 6800 Ω.
Calcula y escribe con detalle como has calculado cada una de las incertidumbres de las medidas realizadas:
Cálculo de ΔRnominal
Cálculo de ΔV. Marca del aparato: Clase del voltímetro:
Error de lectura:
ΔV=
Cálculo de ΔI. Marca del aparato: Precisión del amperímetro:
Error de lectura:
ΔI=
Cálculo de ΔR con Óhmmetro. Precisión del óhmmetro:
Error de lectura:
ΔR=
CUESTIÓN 3: A partir del código de colores calcula la incertidumbre existente en el valor nominal de las resistencias. A partir de las especificaciones de los aparatos calcula las incertidumbres existentes en las medidas de tensión, intensidad y resistencia. Coloca el valor de cada incertidumbre junto al valor medido en la siguiente tabla
|
Rnominal |
Medida de resistencias Montaje largo |
Medida óhmmetro |
||||||
|
R (Ω) |
ΔR |
V(*) |
ΔV |
I(*) |
ΔI |
R=V/I(*) |
R(*) |
ΔR |
|
560 |
|
|
|
|
|
|
|
|
|
1500 |
|
|
|
|
|
|
|
|
|
3300 |
|
|
|
|
|
|
|
|
|
6800 |
|
|
|
|
|
|
|
|
|
12000 |
|
|
|
|
|
|
|
|
|
15000 |
|
|
|
|
|
|
|
|
|
22000 |
|
|
|
|
|
|
|
|
(*) rellenar con datos de la cuestión anterior
A partir de las especificaciones de las aparatos hemos podido calcular la incertidumbre de cada medida realizada. Pero el objeto del montaje largo es la medida de una resistencia aplicando la ley de Ohm, y de esta medida hemos calculado el valor medido pero no su incertidumbre. Cuando obtenemos el valor de una magnitud a partir de una expresión matemática y de la medida de otras magnitudes medidas directamente, decimos que hemos realizado una medida indirecta.
Sea h la magnitud cuyo valor deseamos conocer, y que depende de las magnitudes x, y y z según una expresión matemática h=h(x,y,z). Si las magnitudes x, y y z son medibles directamente y han dado como resultado x±Δx, y±Δy y z±Δz respectivamente, podremos conocer el valor de h tras sustituir los valores medidos de x, y y z en la expresión anterior y su incertidumbre a partir de la expresión:
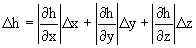
CUESTIÓN 4: Determina la expresión de la incertidumbre para la medida de una resistencias a partir de la ley de Ohm, teniendo en cuenta que el resultado experimental de medir la intensidad es I±ΔI y el de medir la tensión es V±ΔV.
CUESTIÓN 5: Aplica la expresión anterior para calcular la incertidumbre en la medida con el montaje largo de cada una de las resistencias, y coloca su valor en la casilla correspondiente:
|
Rnominal |
Medida de resistencias Montaje largo |
Medida óhmmetro |
|||||||
|
R (Ω) |
ΔR(*) |
V(*) |
ΔV(*) |
I(*) |
ΔI(*) |
R=V/I(*) |
ΔR |
R(*) |
ΔR(*) |
|
560 |
|
|
|
|
|
|
|
|
|
|
1500 |
|
|
|
|
|
|
|
|
|
|
3300 |
|
|
|
|
|
|
|
|
|
|
6800 |
|
|
|
|
|
|
|
|
|
|
12000 |
|
|
|
|
|
|
|
|
|
|
15000 |
|
|
|
|
|
|
|
|
|
|
22000 |
|
|
|
|
|
|
|
|
|
(*) rellenar con datos de las cuestiones anteriores
CUESTIÓN 6: A la hora de presentar los resultados experimentales, se debe de ajustar los decimales de acuerdo a las incertidumbres calculadas, de esta forma se da una información más exacta y clara de lo que conocemos. Vuelve a colocar los valores de la tabla anterior pero ajustados según la norma siguiente:
|
ΔX |
ΔX corregido |
|
0.03445 |
0.03 |
|
1.5678 |
1.6 |
|
21045.12 |
21000 |
|
48.903 |
50 |
|
X±ΔX |
ΔX corregido |
|
1.234±0.03 |
1.23±0.03 |
|
156.19±1.6 |
156.2±1.6 |
|
456903±21000 |
457000±21000 |
Puedes encontrar información adicional acerca de la notación a utilizar, así como ejemplos adicionales en el apartado “Notación: cifras significativas” del tema de teoría de errores.
|
Rnominal |
Medida de resistencias Montaje largo |
Medida óhmmetro |
|||||||
|
R (Ω) |
ΔR |
V |
ΔV |
I |
ΔI |
R=V/I |
ΔR |
R |
ΔR |
|
560 |
|
|
|
|
|
|
|
|
|
|
1500 |
|
|
|
|
|
|
|
|
|
|
3300 |
|
|
|
|
|
|
|
|
|
|
6800 |
|
|
|
|
|
|
|
|
|
|
12000 |
|
|
|
|
|
|
|
|
|
|
15000 |
|
|
|
|
|
|
|
|
|
|
22000 |
|
|
|
|
|
|
|
|
|
Al completar la tabla anterior y comparar las medidas realizadas por ambos métodos, montaje largo y óhmmetro, podemos hacer una valoración de cada sistema de medida. Pero una forma de trabajar esta información y obtener una imagen más clara del resultado de nuestra experiencia, consiste en realizar una gráfica que relacione los resultados obtenidos experimentalmente con los que "deberíamos" haber obtenido: los valores nominales. De esta forma podremos saber si existe alguna desviación sistemática en el conjunto de medidas no achacable a un error accidental, que debe ser aleatorio. Así, por ejemplo, de existir un error de calibración en uno de los aparatos, obtendríamos valores en la medida siempre superiores o inferiores al valor que se desea medir.
En el apartado "Representaciones gráficas de datos experimentales" del tema “Tratamiento de datos experimentales” puedes encontrar instrucciones para la correcta realización de gráficas de datos experimentales.
CUESTIÓN 7: Traza la curva que representa los valores medidos con el óhmmetro en relación a los valores nominales, situando estos últimos en el eje de abscisas.
Marca claramente los puntos experimentales y dibuja asimismo los rectángulos de error, dado que estos representan el resultado experimental que has obtenido.
Traza una curva que sea coherente con el resultado experimental obtenido
En la gráfica, la bisectriz representa el resultado que habrían obtenido si la medida fuese perfecta. Dibujar la bisectriz ayudará a la hora de valorar el sistema de medida.
CUESTIÓN 8: De manera análoga a la gráfica anterior, dibuja los puntos experimentales con sus rectángulos de error y traza la curva que representa los valores medidos con el montaje largo en relación a los valores nominales, situando estos últimos en el eje de abscisas.
CUESTIÓN 9: De los dos sistemas de medida utilizados (óhmmetro y montaje largo) ¿cuál te parece más exacto? ¿Has encontrado en alguno de ellos alguna desviación que no sea aleatoria y por lo tanto no sea asignable a un error de tipo accidental? De ser así, indica cómo afecta al resultado.
| Range |
Accuracy |
| 300 mV 3 V 30 V 300 V 1000 V |
0.025 % + 2 0.025 % + 2 0.025 % + 2 0.025 % + 2 0.025 % + 2 |
| Range |
Frequency |
Accuracy |
All |
20-50 Hz 50 Hz - 10 kHz 10 - 20 kHz 20-50 kHz 50-100 kHz |
1 % + 10 0.2 % + 10 0.5 % + 10 2 % + 20 5 % + 50 |
| Range | Accuracy |
| 30 mA 100 mA 10 A |
0.05 % + 3 0.05 % + 2 0.2 % + 5 |
| Range |
Frequency |
Accuracy |
| mA (to 100 mA) mA (to 100 mA) mA (to 100 mA) A (1-10 A) A (1-10 A) A (0.5 to 1 A) A (0.5 to 1 A) |
20-50 Hz 50 Hz - 10 kHz 10 - 20 kHz 20-50 Hz 50 Hz - 2 kHz 20-50 Hz 50 Hz - 2 kHz |
2 % + 10 0.5 % + 10 2 % + 20 2 % + 10 1 % + 10 2 % + 30 1 % + 30 |
| Range | Accuracy |
| 300 Ω 3 kΩ 30 kΩ 300 kΩ 3 MΩ 30 MΩ 300 MΩ |
0.05 % + 2 + 0.02 Ω 0.05 % + 2 0.05 % + 2 0.05 % + 2 0.06 % + 2 0.25 % + 2 2 % |
| Range | Accuracy |
| 100 Hz 10 kHz 100 kHz 1000 kHz 1 MHz |
0.05 % + 2 0.05 % + 1 0.05 % + 1 0.05 % + 1 Not Specified |
|
|